Welcome to STA 240!

Probability for Statistical Inference

John Zito

Duke University
STA 240 Fall 2025

Course admin

Office hours

Mug	Name	Role	Office Hours
	Hu, Yuang	TA	Mon 7:30 PM - 9:30 PM
	Liu, Aurora	Head TA	WeTh 4:30 pm - 5:30 pm
	Ma, Liane	TA	Sun 10:00 am - 12:00 pm
	Zito, John	Instructor	Tue 3:00 pm - 6:00 pm

Problem Set 0…wtf?

• Low stakes: worth fewer points than other problem sets;

  • (but it will be graded quite rigorously);

• It’s about an 8/10 on the math difficulty scale in this class;

• You will not see much calculus in Weeks 1 - 6 and Midterm 1;

  • (mainly infinite series);

• Serious calculus begins Week 7 and looms large until the end;

  • (be prepared to do some math on Midterm 2 and the Final).

Bottom line

You have until Week 7 to work the kinks out. If, by that time, you are confident that you understand what’s happening on Problem Set 0, then you are ready.

Problem Set 1

• Problems 1 - 3 currently accessible to you;
• Problems 4 - 8 accessible after today’s class;
• Problems 9 - 10 accessible after next week’s classes.

Problem Sets 1 - 4

Each has 10 problems following a “1 + 2 + 5 + 2” structure:

• 1 problem is chatty and conceptual (no math);
• 2 problems practice stuff from 2 weeks ago;
• 5 problems practice stuff from last week;
• 2 problems practice stuff from this week.

So, I lecture on new stuff MoWe, and you have to do two practice problems by that same Friday.

Last time

Set operations

Set	Picture	Logic
\(A\cup B\)		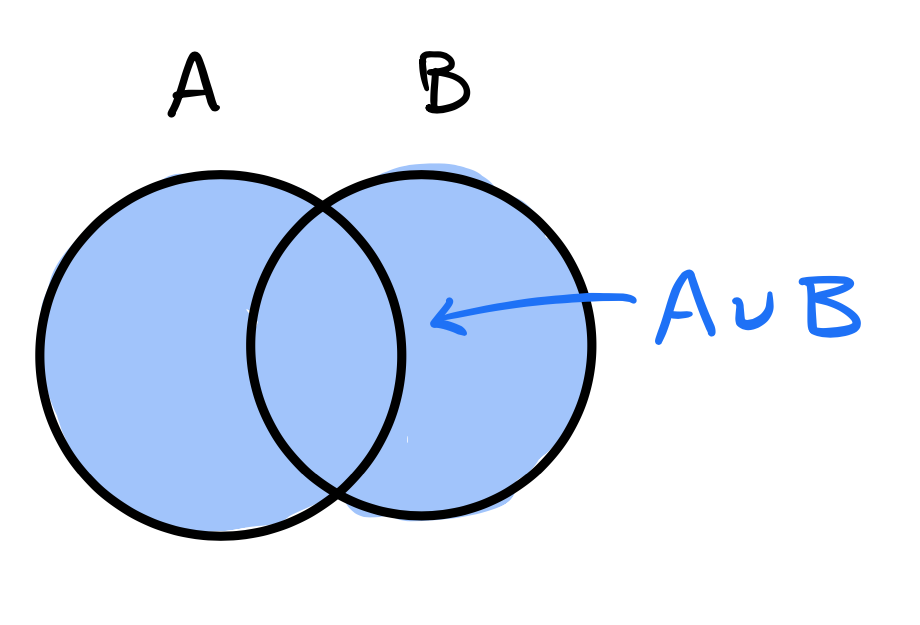(inclusive) OR
\(A\cap B\)		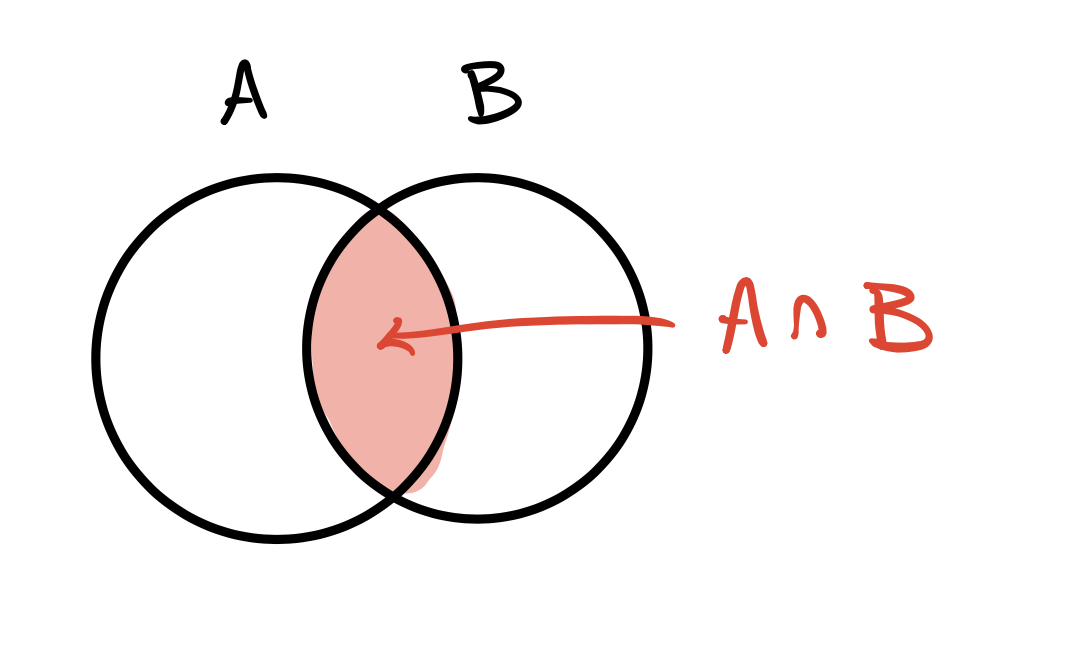AND
\(A^c\)		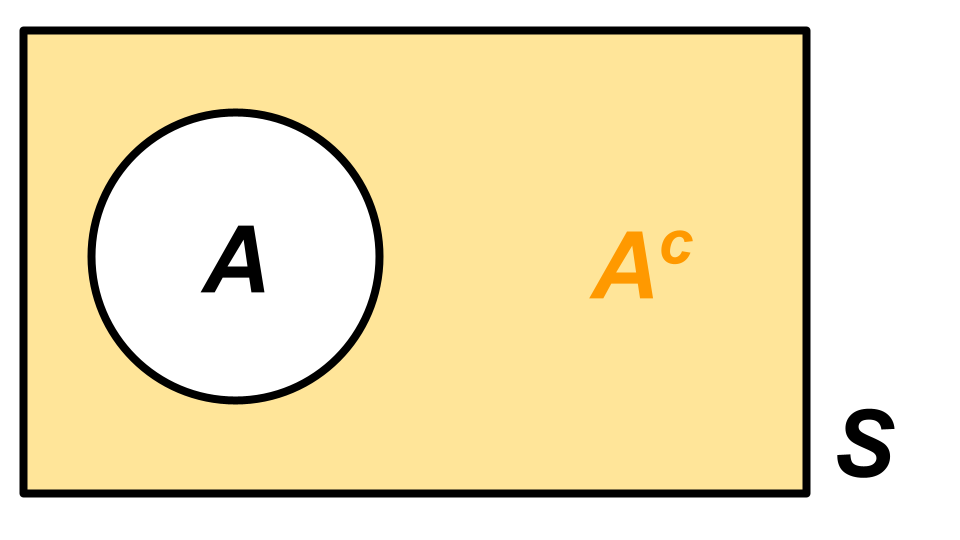NOT

Algebraic properties

\[ \begin{matrix} \text{Commutative} & A\cup B=B\cup A\\ & A\cap B=B\cap A\\ &\\ \text{Associative} & (A\cup B)\cup C = A\cup (B\cup C)\\ & (A\cap B)\cap C = A\cap (B\cap C)\\ &\\ \text{Distributive} & (A\cup B)\cap C = (A\cap C)\cup (B\cap C)\\ &(A\cap B)\cup C = (A\cup C)\cap (B\cup C)\\ &\\ \text{De Morgan's Laws} & (A\cup B)^c=A^c\cap B^c\\ & (A\cap B)^c=A^c\cup B^c. \end{matrix} \]

Probability time

Random phenomena

• the outcome of a coin flip;
• the outcome of a die roll;
• the Poker hand dealt to you from a shuffled deck;
• the outcome of a presidential election;
• whether or not a basketball player makes a free throw shot;
• whether or not my soufflé falls in the oven;
• whether or not the opera singer hits the high note;
• the next song in your Spotify shuffle;
• the next word generated by ChatGPT;
• the birth weight of a newborn child;
• the number of costumers that will arrive at a store or restaurant on a given day;
• when and where a hurricane will make landfall;
• the time until an unstable particle will decay;
• the number of claims an insurance company receives in a month;
• the bid-ask spread of Google stock at 2:37 pm ET next Wednesday.

Why are these things random?

Sample spaces

The set of possible outcomes of a random phenomenon:

Phenomenon	Sample space \(S\)
Flip two coins in order	\(\{HH,\:HT,\:TT,\:TH\}\)
Roll a single die	\(\{1,\:2,\:3,\:4,\:5,\:6\}\)
Card dealt from a shuffled deck	\(\{2\clubsuit,\,3\clubsuit,\,4\clubsuit,\,\ldots\}\)
Winning party in US election	\(\{\text{R}, \text{D}, \text{L}, \text{G}, ..., \text{DSA}\}\)
Your blood sodium level in mEq/L	\(\mathbb{R}_+=(0,\infty)\)
# of insurance claims in a week?	\(\mathbb{N}\)
Return on a risky asset	\(\mathbb{R}\)

Events

A subset \(A\subseteq S\) of the sample space:

Description	Event \(A\)
“the first of two coin flips is a head”	\(\{HH,\:HT\}\)
“the die is even”	\(\{2,\:4,\:6\}\)
“dealt a four”	\(\{4\clubsuit,\,4\heartsuit,\,4\spadesuit,\,4\diamondsuit\}\)
“right-wing party wins”	\(\{\text{R},\,\text{L},\,...\}\)
“blood sodium in healthy range”	\([133,\:145]\)
“over a thousand claims”	\(\{1001,\,1002,\,1003,\,\ldots\}\)
“your investment loses money”	\((-\infty,\:0)\)

Translating set theory into probability

Running example: where will the meteor land?

The sample space is the set of all (long, lat) coordinates in this spatial region:

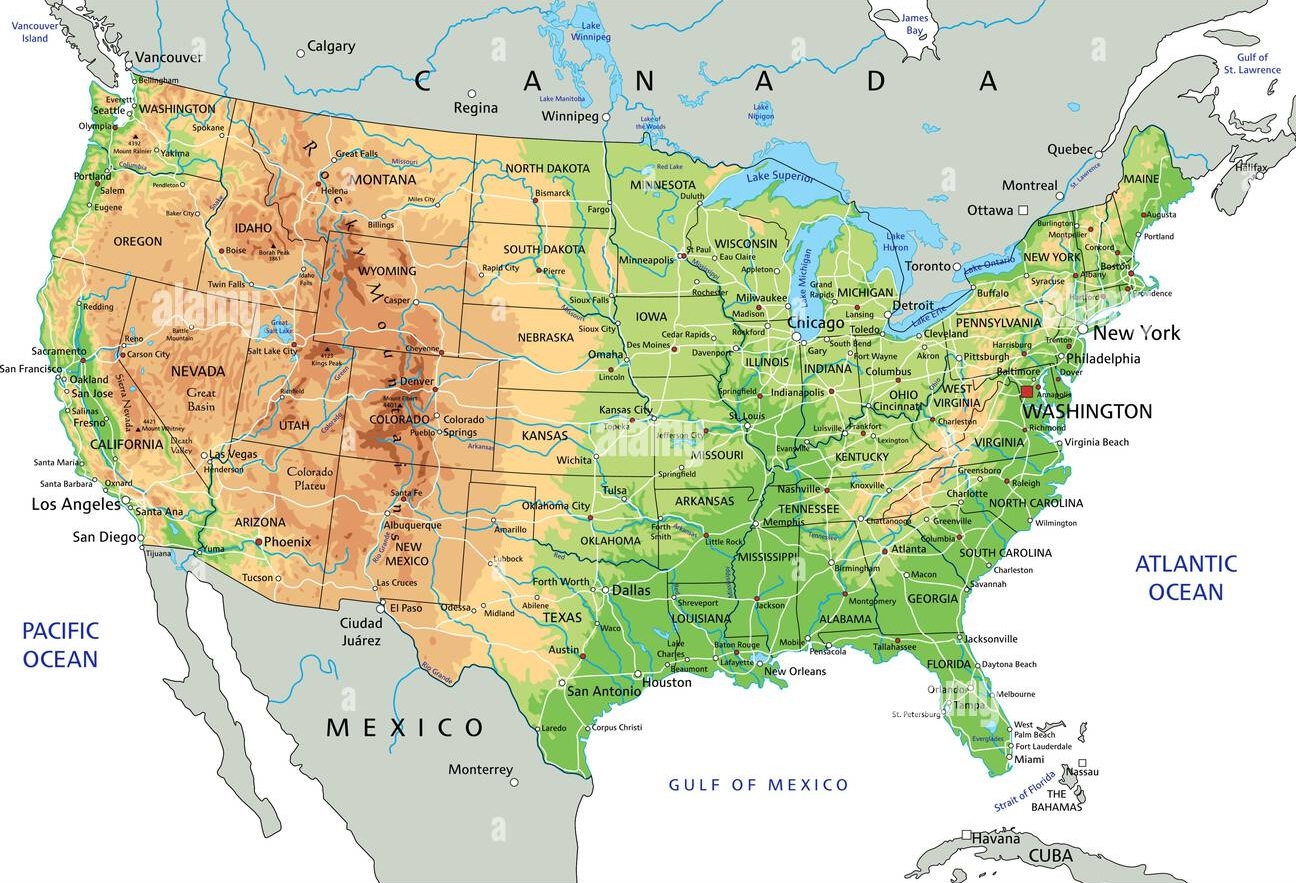
Example events

Symbol	Description
\(A\)	“Meteor lands in the United States”
\(B\)	“Meteor lands in Canada”
\(C\)	“Meteor lands in Mexico”
\(D\)	“Meteor lands in adjacent waters”
\(E\)	“Meteor lands in the Rocky Mountains”

“OR” events (union)

Symbol	Description
\(A\)	“Meteor lands in the United States”
\(B\)	“Meteor lands in Canada”
\(C\)	“Meteor lands in Mexico”
\(D\)	“Meteor lands in adjacent waters”
\(E\)	“Meteor lands in the Rocky Mountains”

• “Meteor lands in the US or Canada”
  → \(A \cup B\)

• “Meteor lands in Mexico or adjacent waters”
  → \(C \cup D\)

• “Meteor lands in the Rocky Mountains or Canada”
  → \(E \cup B\)

• “Meteor lands in North America”
  → \(A\cup B\cup C\)

“AND” events (intersection)

Symbol	Description
\(A\)	“Meteor lands in the United States”
\(B\)	“Meteor lands in Canada”
\(C\)	“Meteor lands in Mexico”
\(D\)	“Meteor lands in adjacent waters”
\(E\)	“Meteor lands in the Rocky Mountains”

• “Meteor lands in the Rocky Mountains and the US”
  → \(E \cap A\)

• “Meteor lands in the US and Mexico”
  → \(A \cap C = \varnothing\)

• “Meteor lands in North America and adjacent waters”
  → \((A \cup B \cup C) \cap D = \varnothing\)

“NOT” events (complement)

Symbol	Description
\(A\)	“Meteor lands in the United States”
\(B\)	“Meteor lands in Canada”
\(C\)	“Meteor lands in Mexico”
\(D\)	“Meteor lands in adjacent waters”
\(E\)	“Meteor lands in the Rocky Mountains”

• “Meteor does not land in the US”
  → \(A^c\)

• “Meteor does not land in the Rocky Mountains”
  → \(E^c\)

• “Meteor does not land on land at all”
  → \((A \cup B \cup C)^c = D\)

Implication

Symbol	Description
\(G\)	“Meteor lands in Georgia”
\(S\)	“Meteor lands in The South”
\(U\)	“Meteor lands in the United States”
\(N\)	“Meteor lands in North America”

Notice:

\[ G\subseteq S\subseteq U\subseteq N. \]

• If we learn that the meteor landed in The South, that implies that it landed in the USA, which implies that it landed in North America;
• It may or may not have landed in Georgia.

Summary

Probability	Set theory
\(A\) or \(B\) occur	\(A\cup B\)
\(A\) and \(B\) occur	\(A\cap B\)
\(A\) does not occur	\(A^c\)
\(A\) implies \(B\)	\(A\subseteq B\)
\(A\) and \(B\) mutually exclusive	\(A\cap B=\varnothing\)