Rhapsody in R

Exploring the intersection of probability and music

John Zito

Duke Stats

2025-08-09

About me

  • It’s my sixth go-around teaching intro probability;
  • I’m a tad weary of coins, dice, playing cards, etc.

Trying to mix it up

Plenty of applications from the natural and social sciences:

  • Actuarial mathematics;
  • Contested elections;
  • Dating apps;
  • DNA sequencing;
  • Expert witness testimony;
  • Extreme weather;
  • I Ching divination;
  • Investment risk and return;
  • Language models;
  • Papal conclaves;
  • Prediction markets;
  • Quantum mechanics.

But what about the arts?

Stochastic music

AKA: chance or aleatoric music.

  • leaving some aspect of the composition up in the air until the moment of performance;
  • ⭐ simulating a random process to determine what notes to write down.

Iannis Xenakis (1922 - 2001)

  • Studied both traditional Western music and CS, statistical mechanics, stochastic processes, etc;
  • Incorporated these ideas into his compositional process.

Pithoprakta (1956)

Think of each member of a 46-piece string orchestra as a Brownian particle drifting up and down the staff:

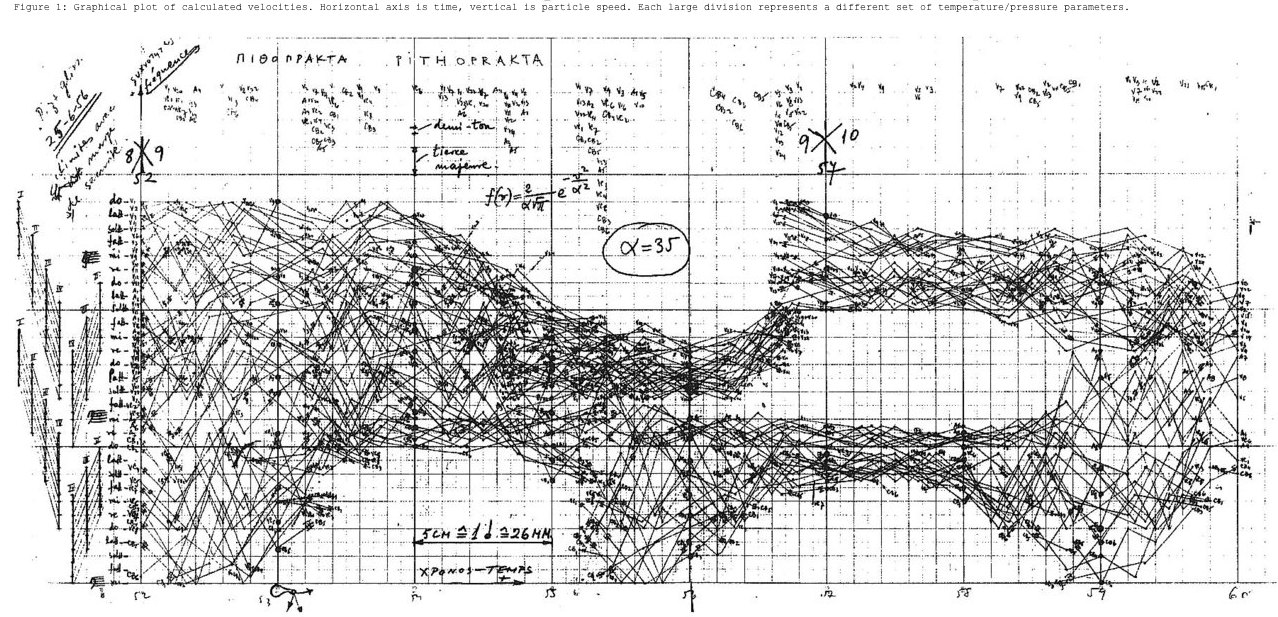
“[E]very member of the orchestra is on the honor system.” Leonard Bernstein

Pithoprakta (1956)

Well …it’s the thought that counts.

Main idea

Thought: Can I prompt students to use what they know about probability distributions and simulation to write their own pieces of stochastic music?

Worry: Depends. Can you work with music in R?

Renfei Mao’s gm package

“grammar of music”

  • Represent music in R with a ggplot2-style interface;

“generate music”

  • integration with MuseScore generates sheet music and MIDI playback.

Ravel: Prélude in A Minor, M. 65

Let’s transcribe it!

The starting point is always the same

We will add layers to this:

library(gm)

prelude <- Music()

Analogous to this:

library(ggplot2)

myplot <- ggplot()

Add meter and tempo

Add meter and tempo

prelude <- Music() + 
  Meter(3, 4) + 
  Tempo(60)

Add the right hand part

Brief aside: scientific pitch notation

"F#5" means the F♯ in the fifth octave on the piano, etc.

Add the right hand part

right_hand <- Line(
  pitches = list(NA, "E5", "F#5", "D5", "E5", "F#5",
                 "B5", "G5", "D5", 
                 "E5", "G4",
                 c("D4", "F#4", "B4"), c("C#4", "F4", "C5"),
                 c("G3", "C4", "E4"), c("D#4", "G4"), c("C4", "E4"))
)

prelude <- Music() + 
  Meter(3, 4) + 
  Tempo(60) +
  right_hand

Add the right hand part

gm::show(prelude)

(BTW: this plays nice with Quarto off-the-shelf.)

Adjust the note values

right_hand <- Line(
  pitches = list(NA, "E5", "F#5", "D5", "E5", "F#5",
                 "B5", "G5", "D5", 
                 "E5", "G4",
                 c("D4", "F#4", "B4"), c("C#4", "F4", "C5"),
                 c("G3", "C4", "E4"), c("D#4", "G4"), c("C4", "E4")),
  durations = c(0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 
                1, 1, 2, 
                1, 1, 
                2, 1, 
                1.5, 0.5, 1)
)

prelude <- Music() + 
  Meter(3, 4) + 
  Tempo(60) +
  right_hand

Adjust the note values

gm::show(prelude)

Add the left hand part

Add the left hand part

left_hand <- Line(
  pitches = c("A2", "E3", "G3", "C4", "E4", 
              "G4", "C5", NA, 
              NA, "E2", "E3", "F#3", "G#3",
              NA, "A2", "E3", "B3", "G3"),
  durations = c(rep(0.5, 7), 2, 
                rep(0.5, 4), 1, 
                rep(0.5, 4), 1),
  bar = 2, offset = 0.5
)

prelude <- Music() + 
  Meter(3, 4) + 
  Tempo(60) +
  right_hand + 
  left_hand + 
  Clef("F")

Note: rests correspond to missing values (NA) in the line.

Add the left hand part

gm::show(prelude)

Add dynamics

Add dynamics

prelude <- Music() + 
  Meter(3, 4) + 
  Tempo(60) +
  right_hand + 
  Dynamic("p", 1) + 
  left_hand + 
  Clef("F") +
  Dynamic("p", 1)

Add expressive indications

Add expressive indications

prelude <- Music() + 
  Meter(3, 4) + 
  Tempo(60) +
  right_hand + 
  Dynamic("p", 1) + 
  Slur(2, 11) + 
  Slur(12, 16) + 
  left_hand + 
  Clef("F") +
  Dynamic("p", 1) + 
  Slur(1, 7) + 
  Slur(10, 13) + 
  Slur(15, 18) + 
  Pedal(1, 7)

Pretty close!

gm::show(prelude)

Change the instrumentation (optional)

prelude <- Music() + 
  Meter(3, 4) + 
  Tempo(65) + 
  right_hand + 
  Dynamic("p", 1) + 
  Slur(2, 11) + 
  Slur(12, 16) + 
  Instrument(47) + # Harp!
  left_hand + 
  Clef("F") +
  Dynamic("p", 1) + 
  Slur(1, 7) + 
  Slur(10, 13) + 
  Slur(15, 18) + 
  Instrument(43) # Cello!

Change the instrumentation (optional)

?Instrument
  1. Acoustic Grand Piano
  2. Bright Acoustic Piano
  3. Electric Grand Piano
  4. Honky-Tonk Piano
  5. Electric Piano 1
  6. Electric Piano 2
  7. Harpsichord
  8. Clavinet
  1. Celesta
  2. Glockenspiel
  3. Music Box
  4. Vibraphone
  5. Marimba
  6. Xylophone
  7. Tubular Bells

… and so on

Change the instrumentation (optional)

gm::show(prelude)

Summary: the gm package

A ggplot2-style interface for music:

prelude <- Music() + 
  Meter(3, 4) + 
  Tempo(65) + 
  right_hand + 
  Dynamic("p", 1) + 
  Slur(2, 11) + 
  Slur(12, 16) + 
  Instrument(47) +
  left_hand + 
  Clef("F") +
  Dynamic("p", 1) + 
  Slur(1, 7) + 
  Slur(10, 13) + 
  Slur(15, 18) + 
  Instrument(43) 
gm::show(prelude)

Thanks Renfei!

Now, let’s write some crazy music!

Every pitch on the piano

pitches <- c("C", "C#", "D", "D#", "E", "F", "F#", "G", "G#", "A", "A#", "B")
octaves <- 1:7
all_pitches <- c("A0", "A#0", "B0", 
                 paste(rep(pitches, length(octaves)), 
                       sort(rep(octaves, length(pitches))), 
                       sep = ""), 
                 "C8")
all_pitches
 [1] "A0"  "A#0" "B0"  "C1"  "C#1" "D1"  "D#1" "E1"  "F1"  "F#1" "G1"  "G#1"
[13] "A1"  "A#1" "B1"  "C2"  "C#2" "D2"  "D#2" "E2"  "F2"  "F#2" "G2"  "G#2"
[25] "A2"  "A#2" "B2"  "C3"  "C#3" "D3"  "D#3" "E3"  "F3"  "F#3" "G3"  "G#3"
[37] "A3"  "A#3" "B3"  "C4"  "C#4" "D4"  "D#4" "E4"  "F4"  "F#4" "G4"  "G#4"
[49] "A4"  "A#4" "B4"  "C5"  "C#5" "D5"  "D#5" "E5"  "F5"  "F#5" "G5"  "G#5"
[61] "A5"  "A#5" "B5"  "C6"  "C#6" "D6"  "D#6" "E6"  "F6"  "F#6" "G6"  "G#6"
[73] "A6"  "A#6" "B6"  "C7"  "C#7" "D7"  "D#7" "E7"  "F7"  "F#7" "G7"  "G#7"
[85] "A7"  "A#7" "B7"  "C8"

The simplest piece of stochastic music

Sample the pitches with replacement:

set.seed(8675309)

line1 <- Line(
  pitches = sample(all_pitches, 64, replace = TRUE),
  durations = .25
)

line2 <- Line(
  pitches = sample(all_pitches, 64, replace = TRUE),
  durations = .25
)

kitten <- Music() + 
  Meter(4, 4) + 
  Tempo(120) + 
  line1 + 
  line2 + 
  Dynamic("p", 1) +
  Dynamic("ffff", 64) +
  Hairpin("<", 2, 63)

(Angry) Kitten on the keys

What is a melody? (wrong answers only)

It’s a time series!

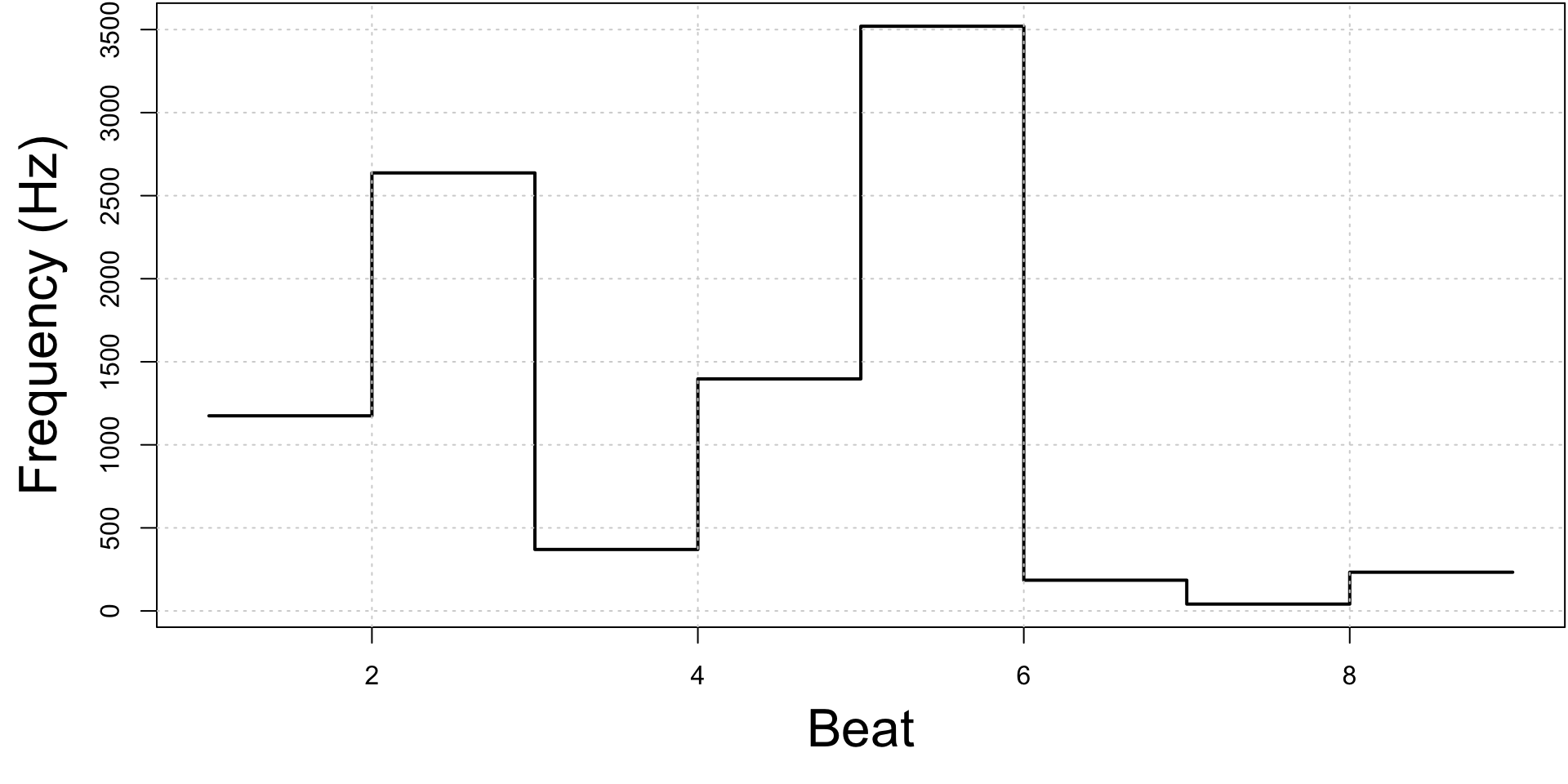
Game:

  • Fix a key (C minor) and a stable accompaniment (waltz);
  • Simulate a melody from a Markov chain.

Un(Markov)chained melodies

From Nierhaus’ Algorithmic Composition (2009 Springer):

Un(Markov)chained melodies

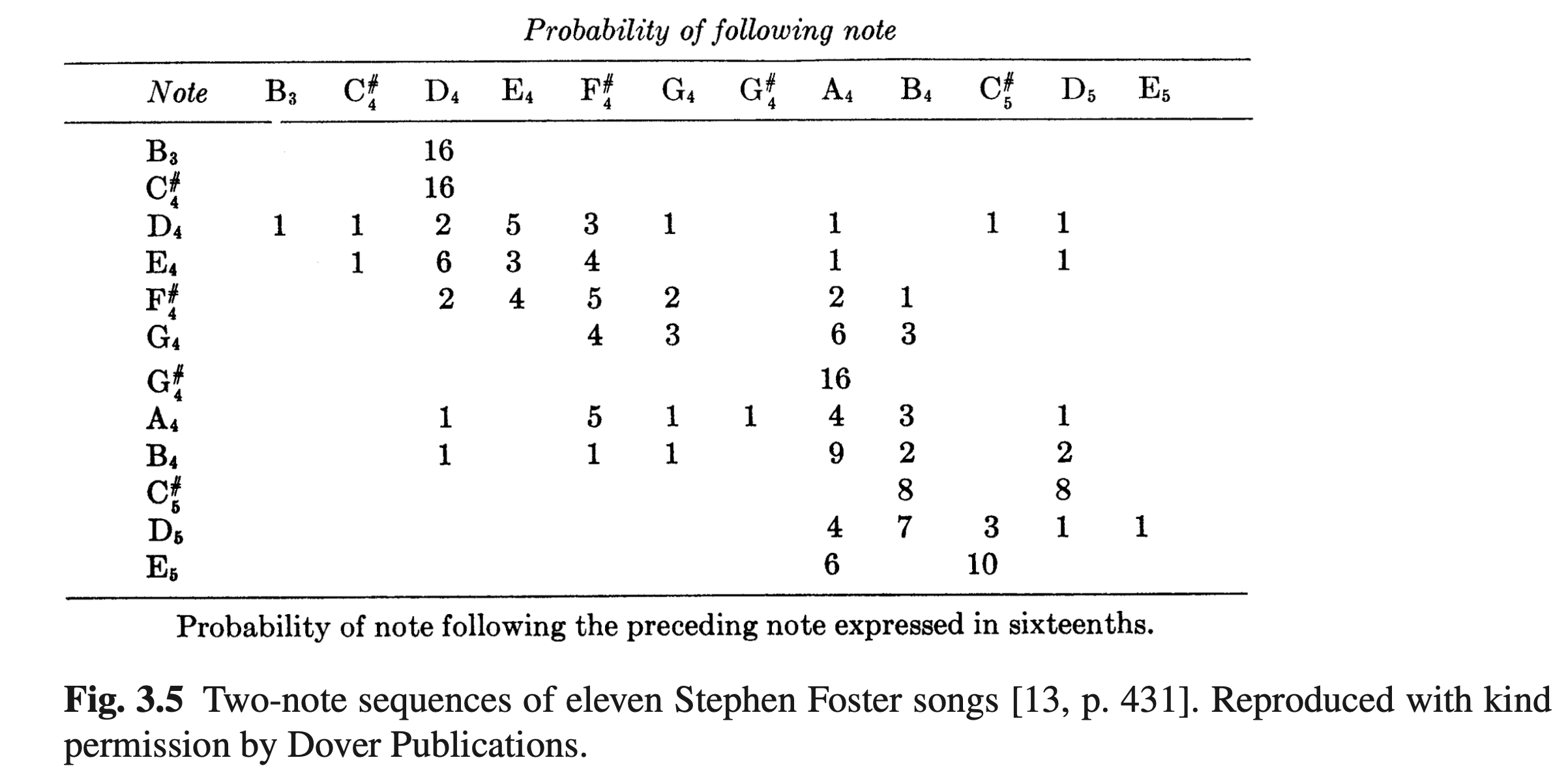
A first-order Markov chain on the C minor scale is described by its transition probabilities: given the note we’re on right now, what are the probabilities for the next note to come?

Loads of options to explore:

  • uniform (sampling with replacement, again);
  • upweight leaps into “chord tones;”
  • upweight leaps between chord tones (arpeggio-like);
  • upweight leaps into the tonic (“resolutions”);
  • random walk (flip a coin every beat and move \(\pm1\)).

IID Melody

Random walk melody

Favors leaps between chord tones

The Jacobson method

Take an existing piece of music and “add noise.”

So this:

\[ \mathbf{y}=f(\mathbf{x})+\boldsymbol{\varepsilon}, \]

only…it’s music?

Name that tune

The students’ mission

  • Write your own piece of stochastic music;
  • Explore the relationship between the probability rules governing the system and the sound of the resulting music;
  • Key words:
    • Play;
    • Surprise yourself.

Randomizing the rhythm

I just like how this looks

Playing with texture

(John, please don’t forget to lower the volume on this.)

They called it “Nightmare Ballet”

Just trolling me

Not quite random, and yet…

Future improvements

  • Can gm handle any Hz, and not just the discrete pitches of the Western system?
  • How closely can I replicate Xenakis’ methods?
  • Play with Markov melodies based on estimated transition probabilities from famous composers;
  • Randomize other features: harmony, rhythm, articulation, orchestration, dynamics, etc;
  • Students need more time and better coaching/inspiration;
  • How can I make it sillier?

Quick takeaways

  • Intro probability is a mixed audience. I aim for maximum variety in the examples and applications;
  • If you as an instructor have any creative or artistic interests, mix them in. You will have a tremendous amount of fun;
  • Activities like this totally tilt the material on its ear;
  • The gm package is so much fun to play with!

Thank you!