Integration
Crudely, the definite integral of a function gives you the (signed) area between the graph of the function and the \(x\)-axis.
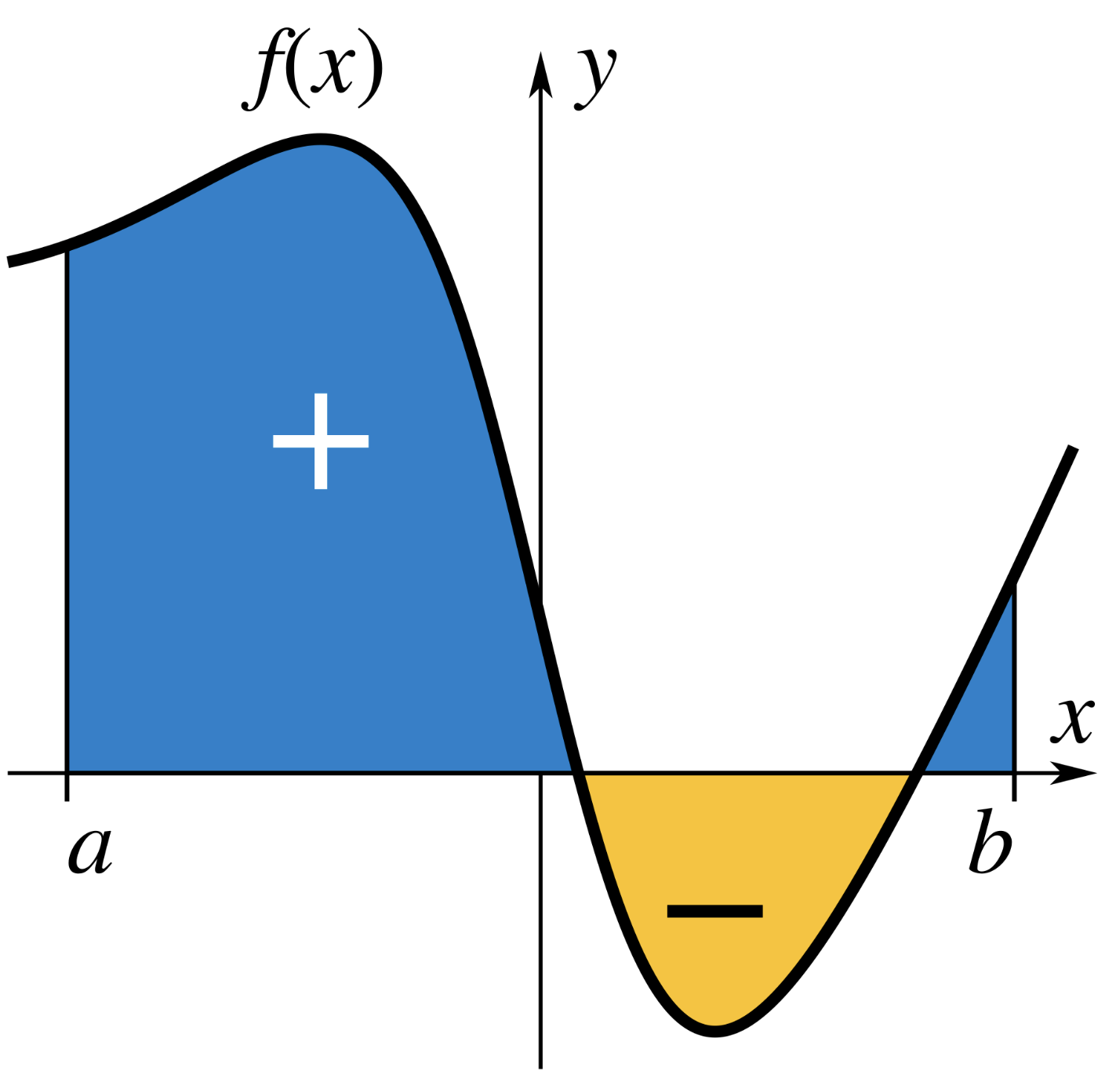
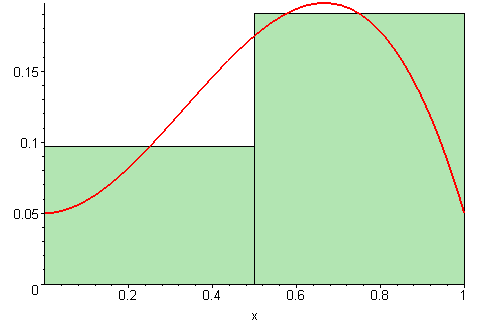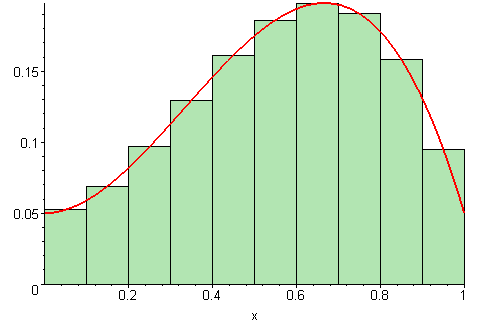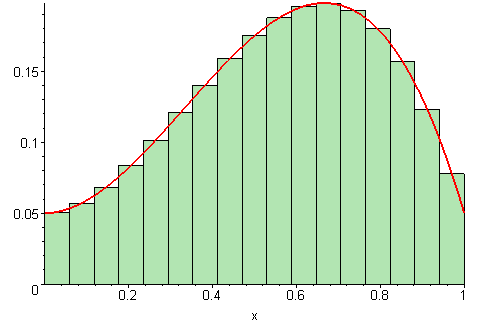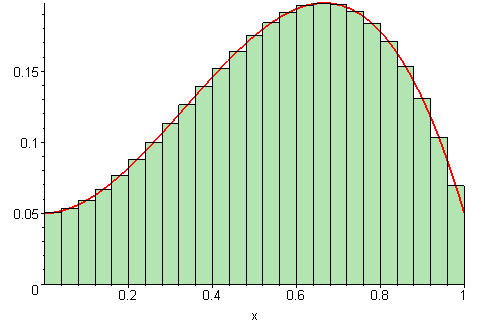
When it exists, which it doesn’t always, the definite integral can be defined as the limit of Riemann sums:
\[ \int_a^b f(x)\,\text{d}x=\lim_{\Delta x\to 0}\sum\limits_{i=1}^n f(x_i^*)\Delta x. \]
Just as the derivative is the continuous analog to a discrete difference, the integral is the continuous analog to a discrete sum.
Integral rules
| rule | formula |
|---|---|
| dummy variable | \(\int_a^bf(x)\,\text{d}x=\int_a^bf(t)\,\text{d}t=\int_a^bf(u)\,\text{d}u=\cdots\) |
| opposite | \(\int_a^bf(x)\,\text{d}x=-\int_b^af(x)\,\text{d}x\) |
| scaling | \(\int_a^bcf(x)\,\text{d}x=c\int_a^bf(x)\,\text{d}x\) |
| sum/difference | \(\int_a^b[f(x)\pm g(x)]\text{d}x=\int_a^bf(x)\,\text{d}x \pm\int_a^bg(x)\text{d}x\) |
| linearity | \(\int_a^b[p\cdot f(x)\pm q\cdot g(x)]\text{d}x=p\int_a^bf(x)\,\text{d}x \pm q\int_a^bg(x)\text{d}x\) |
| split | \(\int_a^bf(x)\,\text{d}x=\int_a^cf(x)\,\text{d}x+\int_c^bf(x)\,\text{d}x\) |
The fundamental theorem of calculus
The fundamental theorem of calculus is a bridge between the seemingly unrelated worlds of derivatives and integrals:
\[ \int_a^bf(x)\,\text{d}x=F(b)-F(a),\quad f(x)=F'(x). \]
On a practical level, it provides a route for evaluating definite integrals by antidifferentiation. The function you are trying to integrate (called the integrand) is \(f\). You imagine \(f\) is the derivative of some function \(F\) which you don’t yet know. If you can “undo” the differentiation and figure out what \(F\) is, then you can evaluate the integral.
Example: antidifferentiation
Consider \[ \int_1^2\frac{1}{x^2}\,\text{d}x. \] What function, when you take its derivative, gives you \(1/x^2=x^{-2}\)? To answer that, you’re essentially undoing the power rule. After a while, you realize \[ \frac{\text{d}}{\text{d}x}\left(-\frac{1}{x}\right)=\frac{1}{x^2}, \] and so
\[ \int_1^2\frac{1}{x^2}\,\text{d}x=\left[-\frac{1}{x}\right]_1^2=-\frac{1}{2}-\left(-\frac{1}{1}\right)=\frac{1}{2}. \]
Integration by substitution
When you perform a \(u\)-substitution, you’re basically trying to undo the chain rule:
\[ \int_a^bf(g(x))g'(x)\,\text{d}x=\int_{g(a)}^{g(b)}f(u)\,\text{d}u. \]
The goal is ultimately to rewrite the integral in a nicer form so that you can recognize what the appropriate antiderivative is and then apply the FTOC.
Example: \(u\)-sub
Check out this ugly thing:
\[ \int_0^2 \frac{x}{\sqrt{x^2+1}}\,\text{d}x. \]
It’s actually not too bad if you make the right substitution: \(u=x^2+1\) and \(\text{d}u=2x\,\text{d}x\). Then you can polish it off by undoing the power rule:
\[ \begin{aligned} \int_0^2 \frac{x}{\sqrt{x^2+1}}\,\text{d}x &= \frac{1}{2}\int_1^5\frac{\text{d}u}{\sqrt{u}} \\ &= \frac{1}{2}\left[2u^{1/2}\right]_1^5 \\ &= \frac{1}{2} \left(2\sqrt{5}-2\sqrt{1}\right) \\ &= \sqrt{5}-1. \end{aligned} \]
Please please please do not forget to change the bounds of the integral when you do a substitution. We had \(u=g(x)=x^2+1\), so after the change of variables, the lower bound becomes \(g(0)=1\) and the upper bound becomes \(g(2)=5\).
Integration by parts
Let’s face it; this sucks. But sometimes you have to integrate a funky product, and there’s no way around it, so you do this:
\[ \int_a^b u(x) v'(x) \, \text{d}x = \left[u(x) v(x)\right]_a^b - \int_a^b v(x)u'(x) \, \text{d}x \]
Through the subtlest of black magic, you have to decide what parts of the integrand to treat as \(u\) and \(\text{d}v=v'\,\text{d}x\). Typically you make \(u\) something that is easy to differentiate, and you make \(\text{d}v\) something that is easy to antidifferentiate. Good luck!
Example: IBP
Consider this integral:
\[ \int_1^2\frac{\ln(x)}{x^2}\text{d}x \] \(\ln(x)\) is easier to differentiate, and \(1/x^2\) is easier to antidifferentiate, which suggests the following choice:
\[ \begin{aligned} u&=\ln(x)\\ \text{d}u&=\frac{\text{d}x}{x}\\ v&=-x^{-1}\\ \text{d}v&=x^{-2}\,\text{d}x. \end{aligned} \]
Let the fun begin:
\[ \begin{aligned} \int_1^2\frac{\ln(x)}{x^2}\text{d}x &= \left[-\frac{\ln(x)}{x}\right]_1^2 + \int_1^2\frac{\text{d}x}{x^2} \\ &= \left[-\frac{\ln(x)}{x}\right]_1^2 + \left[-x^{-1}\right]_1^2 \\ &= \left[-\frac{\ln(2)}{2}-\left(-\frac{\ln(1)}{1}\right)\right] + \left[-\frac{1}{2}-\left(-\frac{1}{1}\right)\right] \\ &= -\frac{\ln(2)}{2} + \frac{1}{2}. \end{aligned} \]
Improper integration (we will do this a lot!)
An improper integral is the limit of a definite integral as one or more of the bounds tend toward some extreme value, typically \(\pm\infty\). So a one-sided improper integral is defined like this:
\[ \int_a^\infty f(x)\,\text{d}x=\lim_{b\to\infty}\int_a^bf(x)\,\text{d}x. \]
A two-sided improper integral is defined as the sum of two one-sided improper integrals, where we make use of the “splitting” property:
\[ \begin{aligned} \int_{-\infty}^\infty f(x)\,\text{d}x &= \int_{-\infty}^c f(x)\,\text{d}x + \int_c^\infty f(x)\,\text{d}x \\ &= \lim_{a\to-\infty}\int_a^cf(x)\,\text{d}x+\lim_{b\to\infty}\int_c^bf(x)\,\text{d}x. \end{aligned} \]
You can pick whatever value of \(c\) is most convenient. Zero will be a common choice.
Example: improper integral with infinite bound
\[ \begin{aligned} \int_0^\infty e^{-x}\,\text{d}x &= \lim_{b\to\infty}\int_0^be^{-x}\,\text{d}x \\ &= \lim_{b\to\infty} [-e^{-x}]_0^b \\ &= \lim_{b\to\infty} \left(-e^{-b}-(-e^{-0})\right) \\ &= -\lim_{b\to\infty}\frac{1}{e^b}+1 \\ &= -0+1 \\ &=1. \end{aligned} \]
Example: improper integral with finite bound
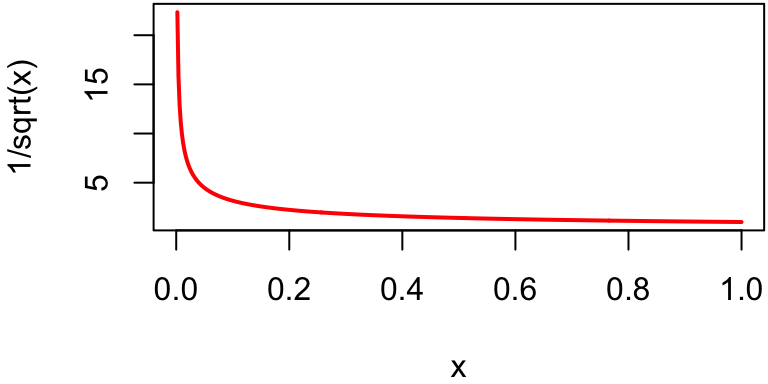
You still might need improper integration, even for an ordinary-looking thing like this:
\[ \int_0^1\frac{1}{\sqrt{x}}\text{d}x. \]
You can see why if you plot the integrand:
There’s a vertical asymptote at \(x=0\), so this is also an improper integral:
\[ \begin{aligned} \int_0^1\frac{1}{\sqrt{x}}\text{d}x &= \lim_{a\to 0}\int_a^1\frac{1}{\sqrt{x}}\text{d}x \\ &= \lim_{a\to 0}\left[2x^{1/2}\right]_a^1 \\ &= \lim_{a\to 0}\left[2\cdot 1^{1/2}-2a^{1/2}\right] \\ &=2-2\cdot0^{1/2} \\ &= 2. \end{aligned} \]
\(2x^{1/2}\) is continuous at 0, so to evaluate the limit you can just plug-in.