Problem Set 2
Due Friday September 19 at 5PM
Before you start
As with Problem Set 1, this problem set asks you to prove new results about how probability measures behave. You are being evaluated on your reasoning and the fluency with which you make use of set theory, the probability axioms, and the various rules we’ve seen (complement, inclusion/exclusion, etc). Please be thorough and explain all of the steps in your logic.
As I mentioned here, the lecture notes on set theory and the probability rules provide a model for how the proofs should look. If you emulate the structure, level of detail, and amount of discussion featured in those examples, you should be good.
Problem 0
Recommend some music for us to listen to while we grade this.
Problem 1
Here is a list of events that may or may not happen, but I believe we will know the final outcome before the end of the semester:
- Zohran Mamdani wins the New York City mayoral election;
- Wicked: For Good makes more money at the box office (inflation adjusted) on its opening weekend than Wicked: Part I;
- The Philadelphia Phillies make it to the 2025 World Series;
- Sean Combs is sentenced to prison for more than 3 years;
- A greater percentage of Duke undergraduates participate in this year’s Duke Marriage Pact than last year’s. About 43% participated last year;
- The total number of points scored at the Countdown to Craziness exhibition game is greater than 50;
- Before the end of the year, the Federal Reserve announces that Lisa Cook is no longer a member of the Board of Governors;
- The United States federal government is shut down due to a lapse in appropriations by October 1, 2025.
Choose three of these, state the probabilities that you assign to the events happening, and explain in a few paragraphs how you formulated your beliefs. What reasoning and evidence did you consider, and how did you weigh it? Feel free to provide links to online sources as needed.
For some of these, you may have strong preferences about the outcome. Try to set them aside and report your honest assessment of the likelihood of the event, whether it pleases you or not.
Problem 2
Let \(A,\,B\subseteq S\) be any pair of events in a sample space \(S\), and show that
\[ \max\{0,\,P(A)+P(B)-1\}\leq P(A\cap B)\leq\min\{P(A),\,P(B)\}. \]
Problem 3
Let \(A_1,\,A_2,\,A_3,\,...\subseteq S\) be an infinite sequence of possibly overlapping events in some probability space. Based on this arbitrary sequence, define a new sequence of events that starts with \(B_1 = A_1\) and then has \(B_i=A_i\cap \left(\bigcup_{j=1}^{i-1}A_j\right)^c\) for all \(i>1\).
Show that the \(B_i\) are pairwise disjoint.
Show that
\[ \bigcup_{i=1}^\infty A_i=\bigcup_{i=1}^\infty B_i. \]
- Use the previous parts to show that
\[ P\left(\bigcup_{i=1}^\infty A_i\right)\leq\sum\limits_{i=1}^\infty P(A_i). \]
Problem 4
Suppose NC license plates are issued at random, each having three letters followed by 4 digits. The current distribution of plates includes all those on which the first letter is either H or J.
- What is the probability that you will get JET-5375? What about HAT-8007?
- What is the probability that you get a plate where the three letters are the same and the four digits are the same?
Problem 5
A box contains 20 balls, 5 each of colors cyan, magenta, yellow and black. Answer the following for an experiment where 10 balls are selected at random without replacement from the box. What is the probability that:
- More than two colors are missing from the selection?
- Magenta and yellow are missing from the selection?
- Exactly two colors are missing from the selection?
- Only the color cyan is missing from the selection?
- Exactly one color is missing from the selection?
- At least one color will be missing from the selection?
- No colors are missing from the selection?
Problem 6
A five-card hand is randomly dealt to you from a well-shuffled deck of 52 standard playing cards. What is the probability that your hand contains exactly two suits?
Problem 7
Let \(B_{10}\) be the set of all length-10 binary strings. So for example, (1, 0, 0, 1, 0, 1, 1, 1, 0, 1) is an element of the set \(B_{10}\). Now, consider that we randomly draw two strings from the set \(B_{10}\) with replacement:
\[ \begin{aligned} \mathbf{a} &= (a_1,\,a_2,\,a_3,\,...,\,a_{10})\in B_{10}\\ \mathbf{b} &= (b_1,\,b_2,\,b_3,\,...,\,b_{10})\in B_{10}. \end{aligned} \]
If we multiply the entries and add
\[ X=a_1b_1+a_2b_2+\cdots +a_{10}b_{10}, \]
what is the probability that the sum \(X\) is equal to \(k\), for each \(k=0,\,1,\,2,\,3,\,...,\,10\)?
- Derive a generic formula for \(P(X=k)\) that is a function of \(k\), but then plug into your formula and produce an \(11\times 2\) table listing the actual decimal numbers for each \(k\);
- Write a lil’ program in
Rthat simulates 10,000 random trials of this phenomenon. Tally up the number of times you get each value of \(k\), and compare the empirical proportions to the actual probabilities in part a. In a large enough number of trials, they should be close by the law of large numbers, which we will study in a month or two.
Problem 8
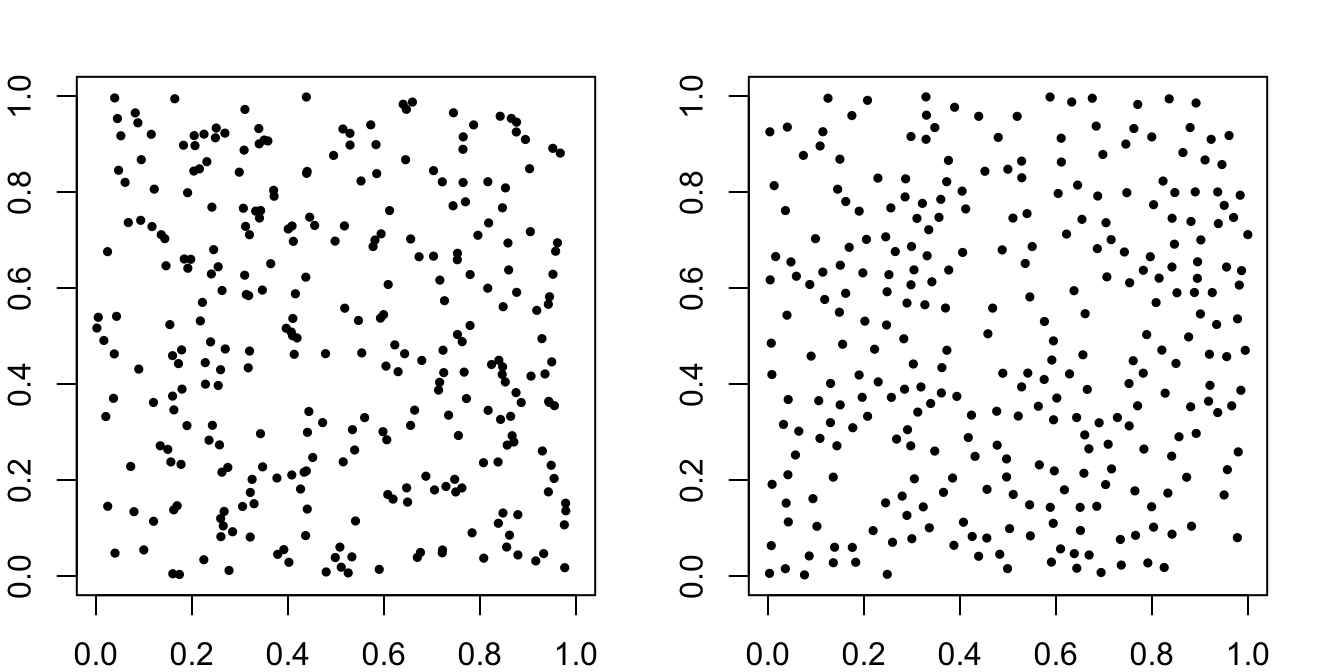
As you may have noticed, Spotify shuffle is not a perfectly random shuffle. If you have a playlist with \(n\) songs, Spotify’s shuffle algorithm definitely does not make all \(n!\) permutations equally likely. Why not? Because people don’t actually want that. Spotify used to implement a pure random shuffle, but users complained that it was too patternful. For better or worse, the human brain is wired to detect meaningless patterns in random noise. For instance, the picture on the left is a “truly” random scatter of points; the one on the right is manipulated so the points don’t “clump”:
When you survey people that don’t know any better, they often feel like the second picture is “more random” than the first because it lacks clumps, but this is a misunderstanding. A truly random playlist shuffle will often have clumps: clumps of artists, clumps of genres, etc. So when people say that they want “random,” what they really mean is just “variety” in some vague sense, and this is what Spotify shuffle tries to deliver. I could not find a good source for what Spotify shuffle currently does, but whatever it is, I personally dislike it.
- Imagine your playlist of \(n\geq 3\) unique tracks contains \(2\leq k\leq \lceil n/2\rceil\) songs by the same artist. What is the probability that a random permutation of the tracks will contain at least one streak of songs by that artist? A streak is two or more of their songs in a row;
- This is the playlist I use when I grade exams (something I enjoy doing, btw). It contains \(n = 14\) songs. There are 11 artists with one song apiece1, and then Chaka Khan has \(k=3\) songs, because, why wouldn’t she? Shuffle this playlist at least twenty times2 and compute the proportion of the time the shuffle contained a “Chaka streak.” Using the previous part, compare this empirical proportion to the theoretical probability that would prevail if the shuffle was truly random.
Problem 9
Pearl Bailey and Elaine Stritch go target shooting. Suppose that each of Pearl’s shots hits a wooden duck target with probability \(p_1\), while each shot of Elaine’s hits it with probability \(p_2\), independent of Pearl. Suppose that they shoot simultaneously at the same target. If the wooden duck is knocked over (indicating that it was hit), what is the probability that both shots hit the duck?
Problem 10
If we know that \(A\) and \(B\) are independent events, show that their complements \(A^c\) and \(B^c\) are also independent events.
Submission
You are free to compose your solutions for this problem set however you wish (scan or photograph written work, handwriting capture on a tablet device, LaTeX, Quarto, whatever) as long as the final product is a single PDF file. You must upload this to Gradescope and mark the pages associated with each problem.
Do not forget to include the following:
- For each problem, please acknowledge your collaborators;
- If a problem required you to code something, please include both the code and the output. “Including the code” can be as crude as a screenshot, but you might also use Quarto to get a nice lil’ pdf that you can merge with the rest of your submission.