Rules for exponents and logarithms

Exponent rules

Let \(a\), \(b\), \(c\), and \(d\) be arbitrary real numbers, and let \(n\) be a positive integer:

\[ \begin{aligned} a^0&=1\\ a^1&=a\\ a^ca^d&=a^{c+d}\\ \frac{a^c}{a^d}&=a^{c - d}\\ a^{-c}&=\frac{1}{a^c}\\ (a^c)^d&=a^{cd}\\ (ab)^c&=a^cb^c\\ \left(\frac{a}{b}\right)^c&=\frac{a^c}{b^c}\\ a^{1/n}&=\sqrt[n]{a}. \end{aligned} \]

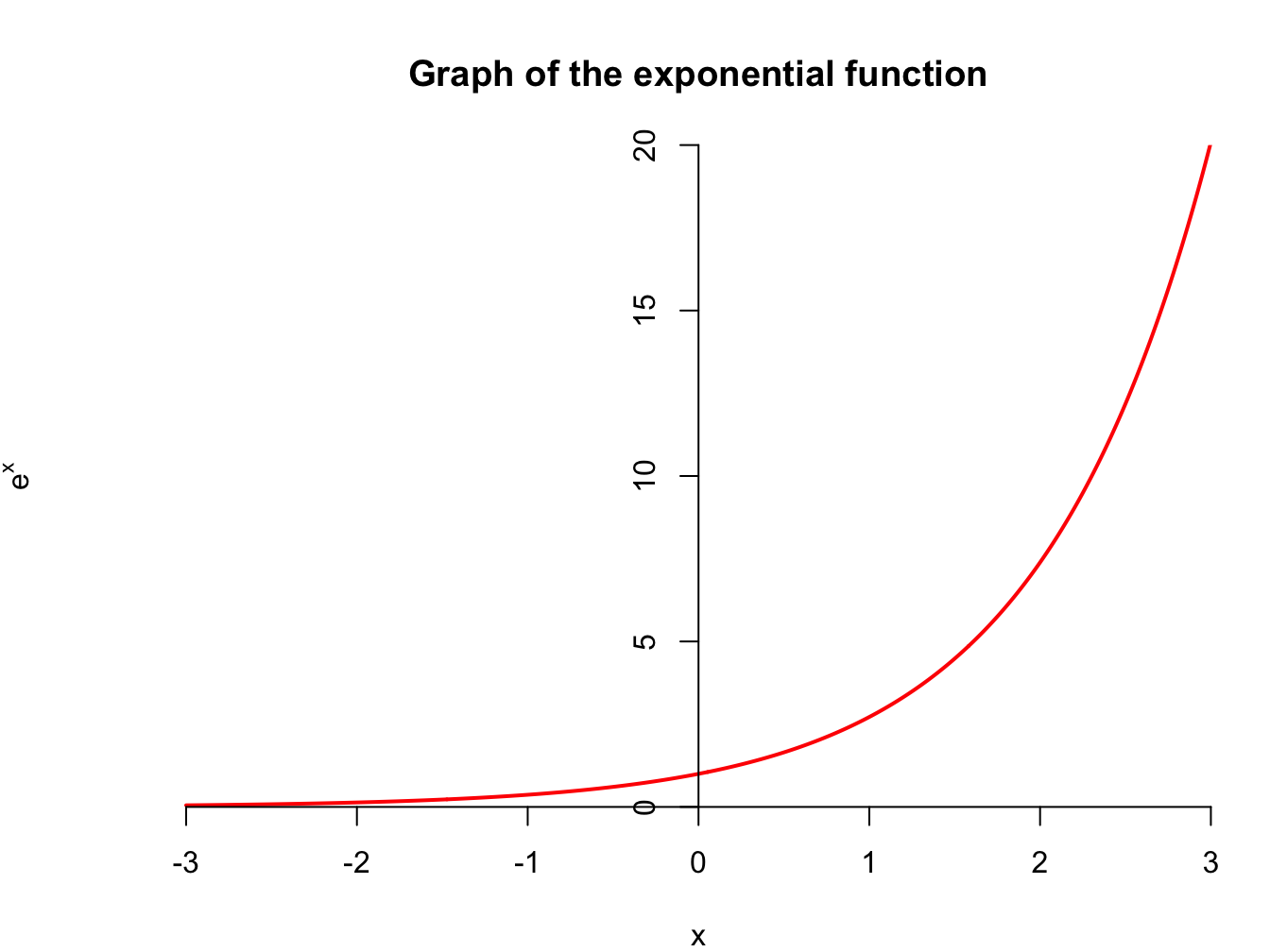
A particularly important function for us is the exponential function \(e^x\), where \(e\approx 2.71828\) is Euler’s number. Because it is defined as an exponent, the exponential function obeys all the rules above: \(e^xe^y=e^{x+y}\), \(e^0=1\), etc.

Here’s the graph of the function:

Code

par(mar = c(4, 4, 4, 0.5))
curve(exp(x), 
      from = -3, 
      to = 3, 
      n = 500, 
      col = "red", 
      lwd = 2,
      yaxt = "n", 
      yaxs = "i",
      bty = "n",
      ylab = expression(e^x),
      main = "Graph of the exponential function",
      ylim = c(0, 20))
axis(2, pos = 0)

A few things to notice:

the exponential is strictly increasing (never plateaus or goes down);
it increases very quickly;
it is defined for all real numbers \(x\);
it is strictly positive: \(e^x>0\) for all \(x\in\mathbb{R}\).

Alternative notation

Sometimes we will write \(\exp(x)\) instead of \(e^x\), but they mean the same thing. We do this to make complicated expressions like this a little easier to read: \[ e^{-\frac{1}{2}\frac{(x-\mu)^2}{\sigma^2}}=\exp\left(-\frac{1}{2}\frac{(x-\mu)^2}{\sigma^2}\right). \]

Logarithm rules

The natural logarithm function \(\ln(x)\) is the inverse of the exponential function \(e^x\). So when we write \(\ln(4)\), we’re asking “\(e\) raised to what power is equal to 4?” Turns out it’s \(\ln(4)\approx 1.386\), so \(e^{1.386}\approx 4\).

Here’s the graph of the function:

Code

par(mar = c(4, 4, 1, 0.5))
curve(log(x), 
      from = 0, 
      to = 8, 
      n = 500, 
      col = "red", 
      lwd = 2,
      xaxt = "n", 
      xaxs = "i",
      bty = "n",
      ylab = "ln(x)",
      main = "Graph of the natural logarithm")
axis(1, pos = 0)

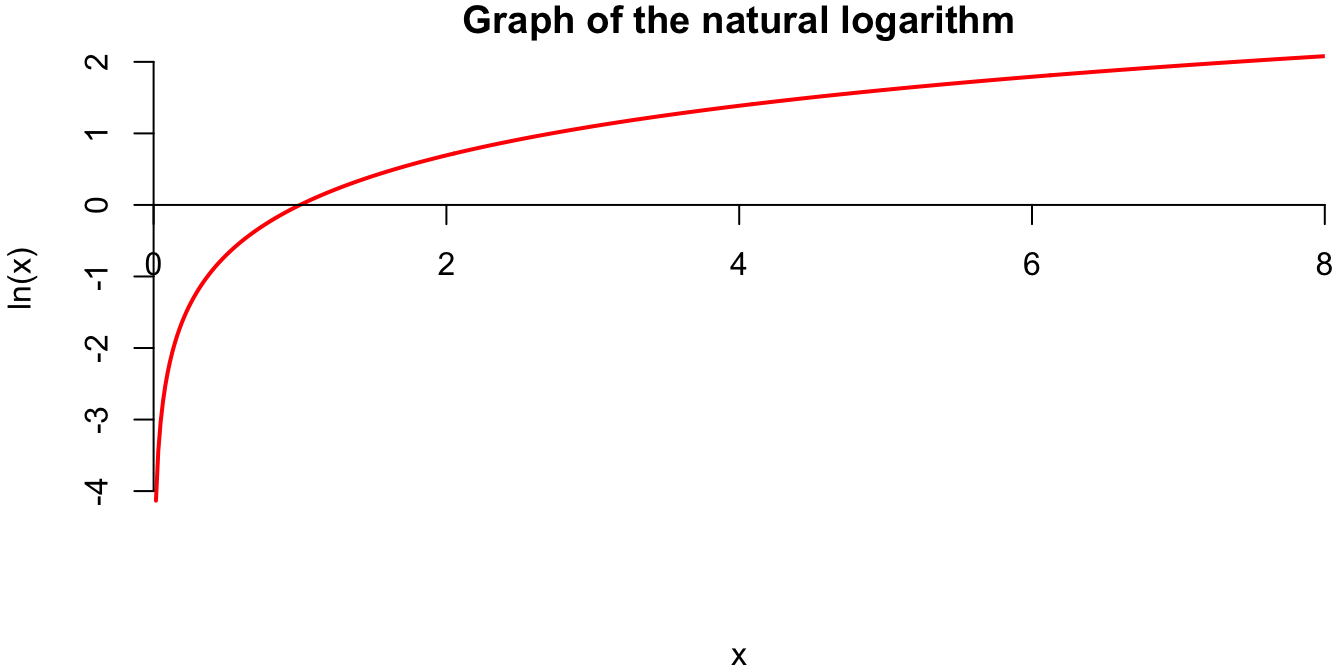
A few things to notice:

the natural log is strictly increasing (never plateaus or goes down);
it increases veeery slowly;
it is only defined for strictly positive numbers;
it returns both positive and negative values;
there is a vertical asymptote at \(x=0\).

So, word to the wise: if you find yourself plugging negative numbers into the natural log, you’ve probably made a mistake someplace.

Anyhow, the natural logarithm has several properties you need to know. Let \(x\) and \(y\) be arbitrary positive numbers, and let \(c\) be any real number (could be negative):

\[ \begin{aligned} \ln(xy)&=\ln(x)+\ln(y)\\ \ln\left(\frac{x}{y}\right)&=\ln(x)-\ln(y)\\ \ln(x^c)&=c\ln(x)\\ \ln(1/x)&=-\ln(x)\\ \ln(e^x)&=x\\ \ln(e)&=1\\ \ln(1)&=0. \end{aligned} \]