Problem Set 3

Due Friday September 26 at 5PM

Problem 0

Recommend some music for us to listen to while we grade this.

Problem 1

Here are some short readings about the case of Sally Clark and Roy Meadow, as well as something called the prosecutor’s fallacy:

Please do the following:

  1. Read the articles;
  2. Using the ideas of conditional probability and independence that we have studied, write a paragraph or two describing what the prosecutor’s fallacy is and how it applies to the Clark case;
  3. If you were an attorney for the defense and had the chance to cross-examine Roy Meadow, what would you ask him about his statistical testimony? What are the most incisive questions you could ask? How would you ensure that the cross-examination would “land” with the members of the jury, who most likely know absolutely nothing about probability and statistics?
Please don’t break my heart

I’m not asking you to read Moby-Dick here.

Problem 2

Poker dice is played by simultaneously rolling five dice. The dice are fair, six-sided, and distinct (imagine that each one is a different color). Find the probabilities of the following dice rolls:

  1. five different numbers;
  2. three of a kind (three dice show the same number, while the other two dice are singles);
  3. full house (three dice show the same number, while the other two show a separate pair).

Problem 3

Consider selecting \(k\) from \(n\) with replacement but ignoring order.

  1. Let’s take the specific case of \(k=2\) and \(n=4\). List out all possible ways you can select \(k=2\) items from \(\{1, 2, 3, 4\}\) in such a scenario.
  2. Let \(x_i\) be the number of times that element \(\{i\}\) is selected, for each \(i = 1,\,2,\,3,\, 4\). For each combination identified in (a), show that it satisfies the following equation:

\[x_1 + x_2 + x_3 + x_4 = 2, \quad x_1, x_2, x_3, x_4 \in \{0, 1, 2\}.\]

  1. State an analogous equation to part b for general \(n\) and \(k\). Use this to show that the number of ways you can select \(k\) from \(n\) with replacement and ignoring order is

\[ \binom{n+k-1}{k}=\frac{(n+k-1)!}{k!(n-1)!}. \]

Problem 4

Let \(S\) be a sample space with probability measure \(P\), and let \(B\subseteq S\) be some event with \(P(B)>0\). Show that the function \(G(A)=P(A\,|\, B)\) is a new probability measure on \(S\). That is, show that \(G\) satisfies the axioms:

  1. total measure 1;
  2. nonnegativity;
  3. countable additivity.

Problem 5

We studied disease testing in class, and in our stylized example, a patient had only two attributes: their true disease status \(D\) and their test result \(T\). In reality of course, patients have many more relevant attributes: genetics, prior medical history, lifestyle, charm and good looks, etc. So in an attempt to be slightly more realistic, we shall extend our little model to include a third attribute: whether or not you have symptoms \(S\).

Table 1 enumerates all of the possible states of the world together with their individual probabilities. These numbers come from a small COVID-19 study of undergraduates in Fall 2020. The test in question is an antigen test. Patients’ “true” disease status was determined by a PCR test that we assume is hella accurate.

Table 1: Some COVID-19 numbers. Source: CDC
\(D\) \(S\) \(T\) \(P(D\cap S\cap T)\)
- - - 0.7650
- - + 0.0128
- + - 0.1685
- + + 0.0018
+ - - 0.0091
+ - + 0.0064
+ + - 0.0073
+ + + 0.0291

  1. What is the overall disease prevalence?

  2. What is the sensitivity of the test?

  3. What is the specificity of the test?

  4. Imagine you develop symptoms. So you visit Dr. Vinnie Boombatz to get tested, and the test comes back positive. Given everything we now know about you, what is the probability that you are truly infected?

  5. What is the overall probability that the test is wrong?

Problem 6

Figure 1

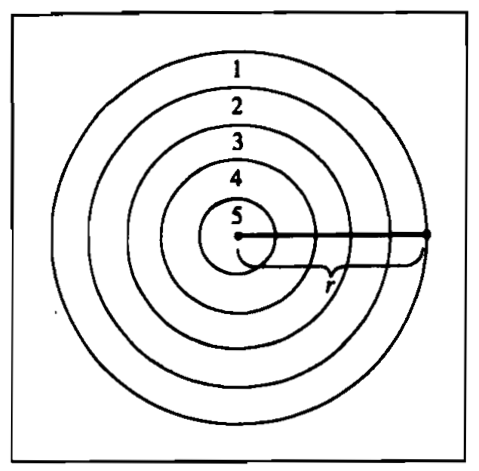
Jerry Lewis is throwing darts at the board pictured in Figure 1. It has the following properties:

  • The board has radius \(r\);
  • The board is partitioned into five rings, each with the same “thickness” \(r/5\);
  • The board is mounted on a wall of area \(A\).

Jerry is not very skilled. His dart is guaranteed to reach the wall and stick someplace, but beyond that, the probability that it lands in any given region is just proportional to that region’s area.

Task: Derive a general formula for the conditional probability that a dart lands in ring \(i\) given that it hits the board and not the wall. Your formula should be a function of \(i=1,\,2,\,3,\,4,\,5\). Check that these probabilities are nonnegative and sum to one.

Problem 7

An encryption algorithm generates a seed value \(z\) in the following way:

  • A binary operator is chosen at random from \(\{+,\,\cdot\}\);

  • Two distinct numbers \(x\) and \(y\) are chosen at random from the set \(\{1,\,2,\,...,\,9\}\) and the binary operation chosen above acts on \(x\) and \(y\) to produce \(z\).

  1. What is the probability that \(z\) is an even number?
  2. You notice that the algorithm generates an even \(z\) value. Given this, what is the probability that the \(+\) operator was used to generate it?

Problem 8

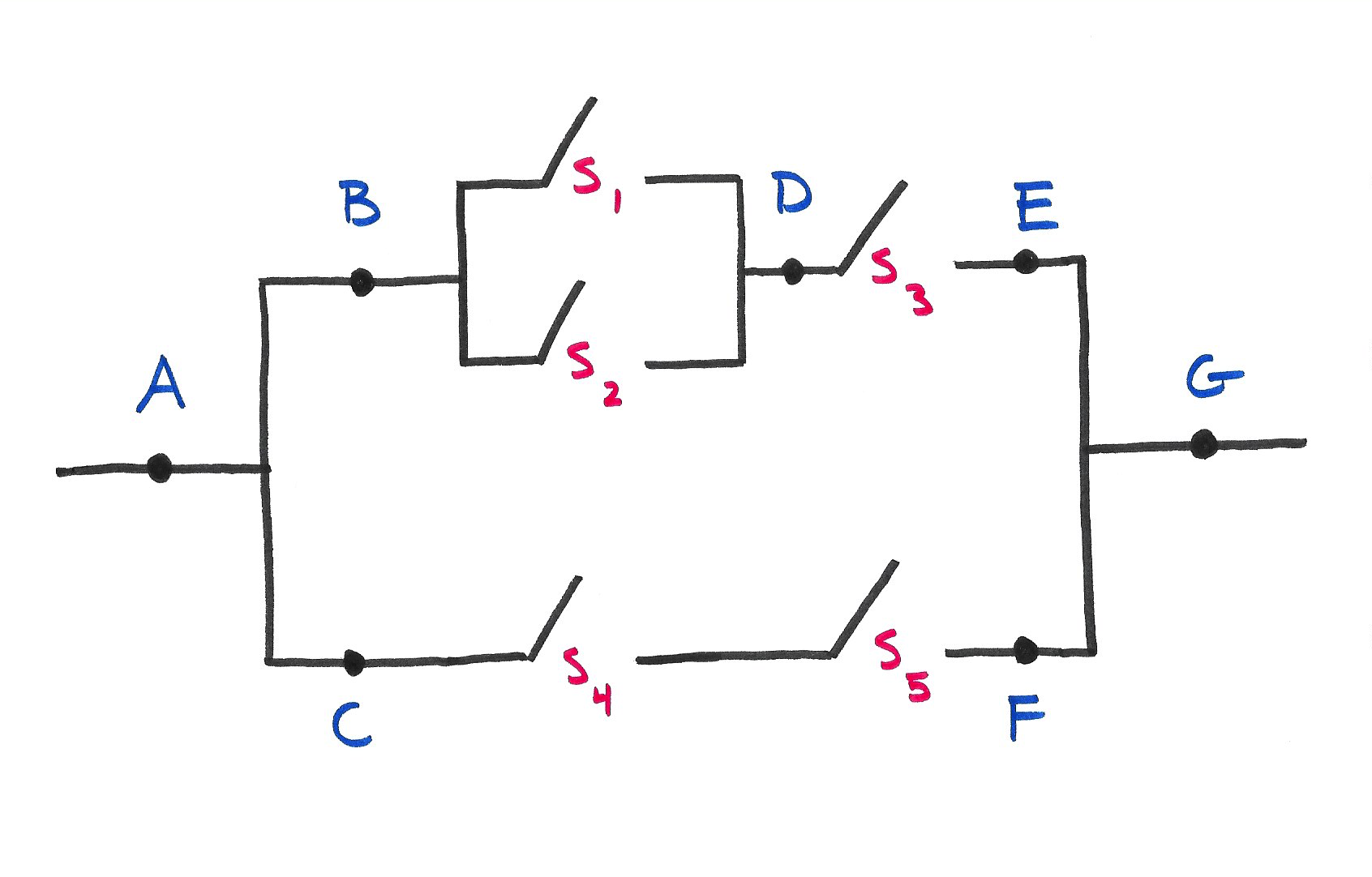
The figure above displays a circuit. Switch \(S_i\) closes with probability \(p_i\), and the switches close independently of one another. What is the probability that electricity can flow from \(A\) to \(G\)?

Problem 9

Two balls are chosen randomly from an urn containing 8 green, 4 black, and 2 orange balls. Suppose that we win $2 for each black ball selected, we lose $1 for each green ball selected, and we earn nothing for each orange ball selected. Let \(X\) denote our winnings.

  1. Make a table with the possible values of \(X\) and the probabilities of each value.

  2. Sketch the pmf of \(X\).

  3. Sketch the cdf of \(X\).

  4. Compute the expected value of \(X\).

Problem 10

I dreamed last night I got on the boat to heaven
And by some chance I had brought my dice along

Guys and Dolls

Alas. You settle in for what you think will be a good night’s beauty sleep, and you end up having one of those awful dreams where you must take a test you haven’t studied for. It’s a multiple choice test, each question has five options with only one correct answer, there are fifty questions in total, and each is worth one point. The god Morpheus has kindly seen fit to leave a fair, five-sided die in your dream pocket, and so your dream self decides to do the only thing you can do: use the die to answer each of the exam questions completely at random.

  1. Let \(X\) be the number of questions you answer correctly. What is the distribution of \(X\)?
  2. Plot the probability mass function of \(X\);
  3. What is the expected number of questions you will answer correctly?
  4. What is the probability that you get at least a C- on the exam?

Submission

You are free to compose your solutions for this problem set however you wish (scan or photograph written work, handwriting capture on a tablet device, LaTeX, Quarto, whatever) as long as the final product is a single PDF file. You must upload this to Gradescope and mark the pages associated with each problem.

Do not forget to include the following:

  • For each problem, please acknowledge your collaborators;
  • If a problem required you to code something, please include both the code and the output. “Including the code” can be as crude as a screenshot, but you might also use Quarto to get a nice lil’ pdf that you can merge with the rest of your submission.