Here is a very silly function:

\[ h(x) = \exp\left(-\frac{1}{2}\frac{(x-\mu)^2}{\sigma^2}\right) ,\quad -\infty<x<\infty . \]

Treat \(-\infty<\mu<\infty\) and \(\sigma>0\) as constants and compute the value(s) of \(x\) at which \(h\) has inflection points.

Hint

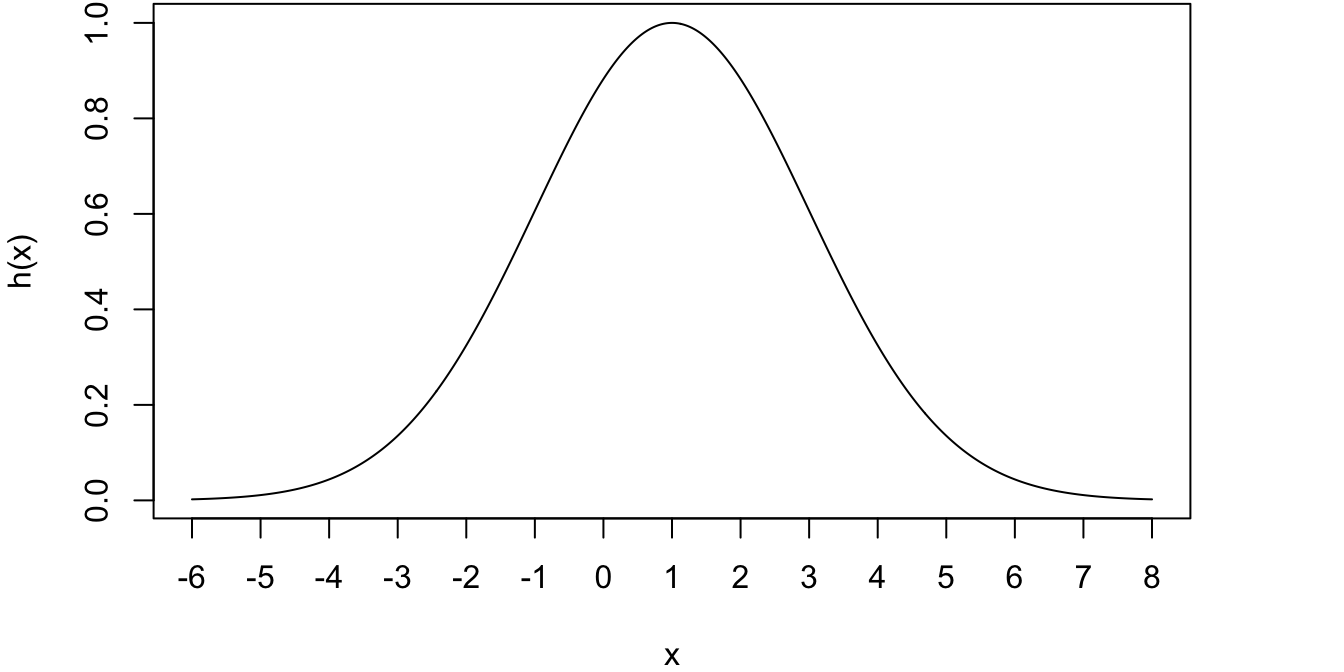
Here is an example of what \(h\) might look like in the special case where \(\mu = 1\) and \(\sigma=2\):

m = 1
s = 2
par(mar = c(4, 4, 0.1, 4))
curve(exp(-0.5 * ((x - m) / s)^2), 
      from = -6, to = 8, n = 500,
      xlab = "x", ylab = "h(x)",
      xaxt = "n")
axis(1, at = -6:8)

Before you start doing any math, can you use the picture to guess what the answer will be?