Quantum mechanics has a reputation for being an intimidating branch of theoretical physics, and JZ certainly doesn’t understand a ding dong thing about it. Even so, because we have studied some basic probability theory, the mathematics of quantum mechanics is more accessible than you might guess. Behold:
Imagine a single particle at the (sub)atomic level1. A particle’s quantum state encodes information about all of its measurable properties, such as position, momentum, spin, and energy. In quantum mechanics, measuring these properties is fundamentally probabilistic. Before measurement, the particle doesn’t have a single, definite position or momentum; it has only probabilities for the possible outcomes. The quantum state of a particle is fully characterized by its wave function, and the squared magnitude of the wave function is a probability density that describes the distribution of the particle’s position, or momentum, or whatever else you wish to study. Let’s explore this in a very simple example.
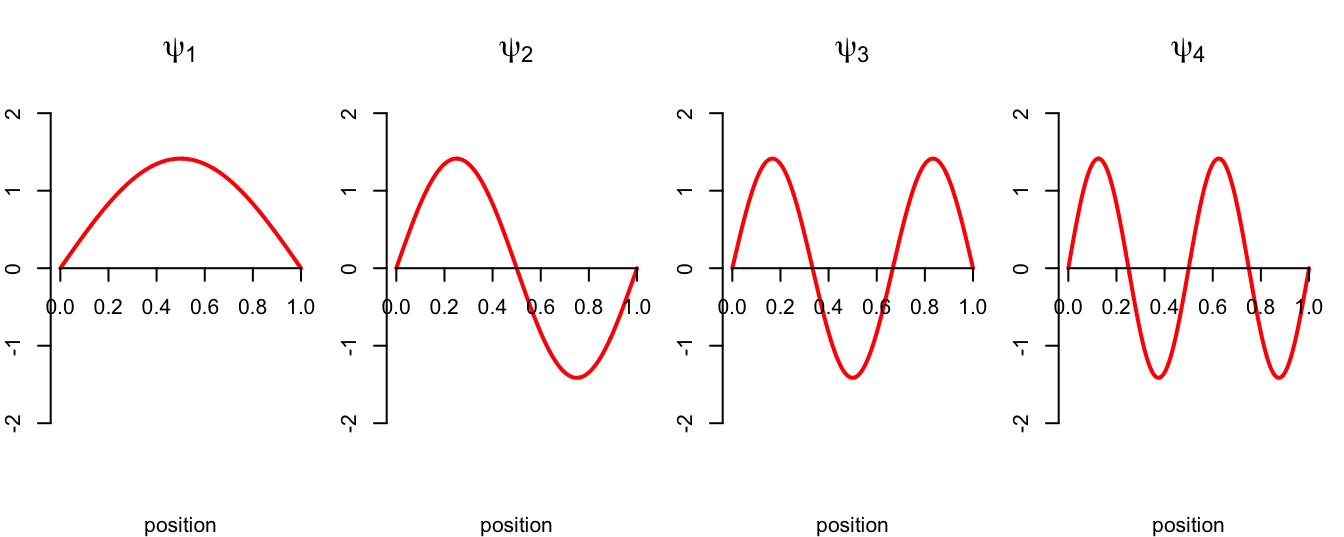
Consider a single, one-dimensional particle located somewhere in the interval \([0,\,L]\). The wave function associated with the particle’s quantum state is
\[ \psi_n(x) = \begin{cases} A\cdot\sin\left(\frac{n\pi}{L}x\right) & 0\leq x\leq L\\ 0 & \text{else}, \end{cases} \]
where \(A\geq 0\) is the amplitude, and \(n=1,\,2,\,3,\,...\) indexes the particle’s energy level. The higher the energy level, the more “excited” the particle is. Behold:
Because the particle does not have a definite position before measurement, we treat the position \(X_n\in[0,\,L]\) of the particle as a continuous random variable whose probability density function is \(f_n(x)=|\psi_n(x)|^2\).
- Compute the value of \(A\) that ensures that \(f_n\) is a valid pdf;
- Compute the cdf of the random variable \(X_n\) and plot it for various values of \(n\);
- What is the expected location of the particle?
- What is the probability that the particle is located at the midpoint of the interval?
- Let \(n=4\) and \(L=1\). What is the probability that the particle is located in the interval \([0.2, 0.3]\)?
- The parameter \(n=1,\,2,\,3,\,...\) indexes the energy level of the particle. The larger the value of \(n\), the more excited the particle is. If \(n\to\infty\), then the particle is, like, super stoked. What happens to the distribution of \(X_n\) as \(n\to\infty\)?
Footnotes
If you’re like me, you cannot do this. Oh well.↩︎
